Carry lookahead Full Adder

 CPU의 연산처리과정 중 그 흔한 덧셈을 어떻게 최적화 시켰을까 궁금하여 찾아보게 된 자료이다.

 

 가산기는 간단히 두 수의 덧셈을 연산하는 논리회로이다. 반가산기, 전가산기 그리고 RCA는 익숙하지 않은 사람이 회로만 확인하여도 이해가 가능할 정도로 간결한 회로이다.

 

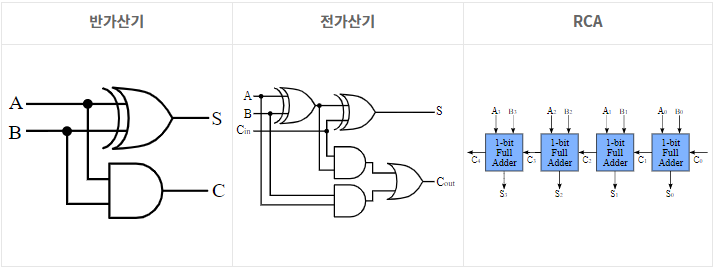
 정리하면 반가산기는 입력으로 두 개의 bits가 주어졌을 경우 sum과 carry bit을 구한다. 전가산기는 반가산기에 carry bit 입력까지 더하였고, RCA는 이러한 전가산기를 여러 bits에서 연산 가능하도록 조합한 형태이다.

 

 RCA로 가산기를 만들었다 생각하고 32bits 덧셈을 하는데 몇 개의 논리게이트를 통과하는지 생각해보자. 1bit의 전가산기를 연산하는데 2단의 논리게이트를 통과하고 자리올림을 확인하기 위해 첫번째 자리부터 순차적으로 계산한다고 하면 32x2=64개의 게이트를 통과해야 한다. 마지막 자리의 carry가 있을 경우 추가 게이트가 필요하므로 65개 이상의 게이트를 통과한다고 볼 수 있다.

 

 자리올림( carry)이 이전 자릿수의 결과값에 의존하기 때문에 병목지점이며 자리올림 문제를 효율적으로 처리해야한다는 생각까지 도달할 수 있다. 해결책으로 예측( CLA, Carry-Lookahead-Adder) 방향으로 나아가야 한다는 것을 알 수 있 다.

 

 CLA, Carry-Lookahead-Adder

자리올림을 예측하기 위하여 다음과 같이 Generate와 Propagate라는 함수를 정의한다.

 

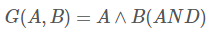
→ 이전의 결과값과 상관없이 자리올림이 발생하는지 확인

 

→이전의 결과값에 따라 자리올림이 발생할 가능성이 있는지 확인

 

 

 $S$( sum)과 $C$( carry)를 구해보자.

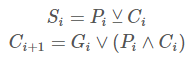
 위 식을 보면 이전 결과값을 기다리는 $C_i$의 식을 재귀적으로 풀면 $G$와 $P$에 관한 식으로 나타낼 수 있다. $G$와 $P$는 식에서 알 수 있듯이 각 bit에 독립적이기 때문에 한 번에 연산이 가능하다. $C_i$를 이전 결과값에 의존적이지 않게 구할 수 있다는 것이다.

 

 하지만 재귀적으로 $C_i$를 풀어보면 $G$와 $P$로 이루어진 꽤나 긴 식이 나오는데 이게 더 오래 걸리는것이 아닌지라는 의구심이 들 수 있다. 여기서 BIT( Binary Indexed Tree)의 개념을 가져오면 빠르게 구할 수 있다.

 

$i$를 $2^x$라고 할 때,

 위와 같이 구간을 확대해가며 $G$, $P$값을 구하면 32bits 기준으로 $O$($\log_2{32}$) 깊이의 논리게이트를 사용해서 모든 $G$와 $P$를 구할 수 있다. 이로써 덧셈에 필요한 모든 값들을 구하였으며 원하는 결과값인 $S_i$를 구할 수 있다.

 

★ BIT :

greeksharifa.github.io/algorithm%20&%20data%20structure/2018/07/09/algorithm-fenwick-tree/#:~:text=%ED%9D%94%ED%9E%88%20BIT%EB%9D%BC%EA%B3%A0%20%EB%B6%88%EB%A6%AC%EB%8A%94%20%ED%8E%9C%EC%9C%85,%EC%9E%88%EB%8F%84%EB%A1%9D%20%EA%B3%A0%EC%95%88%EB%90%9C%20%EC%9E%90%EB%A3%8C%20%EA%B5%AC%EC%A1%B0%EC%9D%B4%EB%8B%A4.

 

마무리

 CLA는 기존의 RCA보다 논리게이트는 더 많이 필요하나 $i+1$를 구하기 위하여 $i$번째 결과를 기다리지 않아도 된다. 32bits의 덧셈의 경우 문제의 $C$를 구하는데 20개 내외의 논리게이트를 사용하므로 CPU의 cycle을 단축시킬 수 있다.